東電福島�T-3号用MOX外径データ分布の異常
-４ミクロンキザミデータから１ミクロンキザミデータを推定(予測)する-

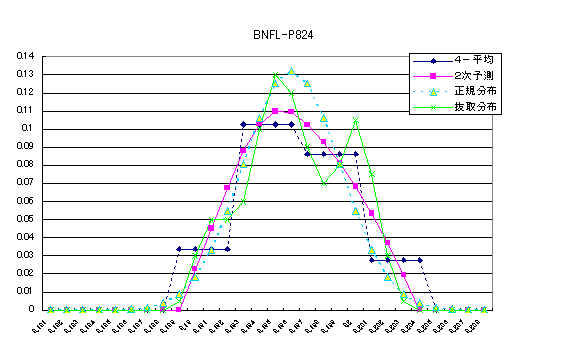
東電はMOXペレットの外径について、１ミクロンキザミのデータがあるのに、それをわざわざ４つずつ足し合わせた4ミクロンキザミのデータしか公表していない。これではデータの異常が隠されてしまう。事実、高浜４号で不正が確定した異常な形のグラフを用いて同じ操作をしてみると、異常性が消えたような形になってしまう。 　そこで小山の第４陳述書では、４ミクロンキザミのデータを使って元の１ミクロンキザミのデータを推定（予測）することを試みている。まず高浜４号の場合を例にとって何をしたかを簡潔に説明しよう。 　下図は、不正が確定している高浜４号のロットP824の外径データ分布に関するものである。緑色グラフが１ミクロンキザミの抜取検査データを示している。これから東電がやったのと同じように、４つずつデータを足し合わせて平均すると、ダイヤ印が横に４つ並んだグラフになる。次に、この平均値しか分からないと想定して、各区分ごとに２次式（放物線）を仮定して元の緑色グラフを推定（予測）すると、ピンクのグラフが求められる。ジグザグな緑色グラフそのものは再現されないが、そのジグザグを平均化した位置を進むような形になっている。もうひとつの三角印（点線）は正規分布グラフであり、これと比べるとピンクグラフは山が下がり右側が膨らんだ形をしている。元の緑グラフで右側に第２の山があることを反映しているためである（どのグラフも、その下の面積＝全確率＝１と規格化されている）。

結局、この推定方法では、元のグラフのジグザグまでは再現されないが、しかし逆に、もしピンクの推定グラフが相当に歪んでいる場合は、元のグラフはそれ以上に歪んでいるはずだと結論できる。 東電の福島�T-3（１F3）の場合、そのような推定グラフが著しく歪んでいる場合が16ロット中に4ロット存在することを確認できる。そのうちの１例を、ロット1604の抜取分布について次に示そう。

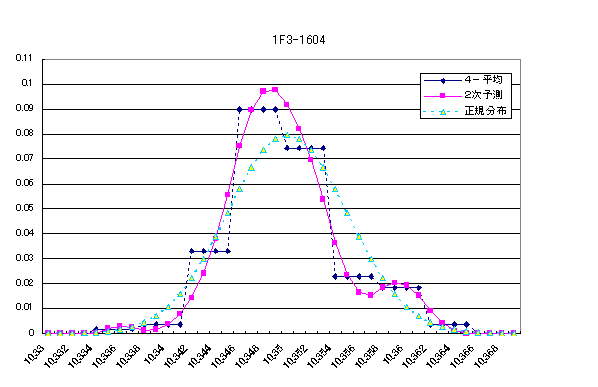ピンクグラフが関電の場合と同じ意味をもつ推定（予測）グラフである。公表された４ミクロンキザミのデータ（ダイヤ印）から推定したものである。明らかに正規分布から著しく歪んで、外径の大きい側に第２の山があるのが見える。高浜４号の場合との比較から分かるように、実際の１ミクロンキザミのグラフは、このピンクグラフよりさらに大きく歪んでいるはずである。 その実際の異常な姿はどうなっているのか、東電は１ミクロンキザミのデータを公開して具体的な姿を示すべきである。そして同時に、その異常がいかなる理由によって起こったのかを具体的に説明しなければならない。それができない場合は、不正がないことの立証責任を放棄したとみなされるべきである。

トップ